本文介绍卷积神经网络（convolutional neural network，CNN）。卷积神经网络是专为图像数据设计的神经网络，其参数小于全连接的网络，而且卷积也便于在GPU中并行计算。因此，CNN广范围研究人员采用。CNN较为重要，因此分两篇文章介绍。

从全连接层到卷积

多层感知机适合处理表格数据，其中每行对应一个样本，每列对应样本的特征或标签。样本的不同特征之间可能有交互，所以适合采用多层感知机。如果对于图像等高位数据，这种网络可能不可用。例如，如果有一个图像数据集，其中每个图像的像素为一百万，虽然从生活角度讲，一百万像素的图像清晰度分辨率非常有限，然而从模型输入角度，意味着输入到模型中每次逗游一百万个维度，全连接层的维度会多到难以想象，这种维度爆炸的情况使得此时训练模型变得不可实现，因此采用全连接层很难对图像数据进行识别学习，考虑采用卷积神经网络方法。

不变性

从日常生活的常识中可以知道，从图像中寻找某个物体，无论用何种方法找到这个物体，都应该和物体的位置无关，这就是空间不变性（spatial invariance），具体包含以下两点：

平移不变性（translation invariance）：无论待检测对象出在图像的什么位置，神经网络的前几层应该对相同的图像区域具有相似的反应，即为平移不变性。
局部性（locality）：神经网络的前几层应该知探索输入图像中的局部区域，而不过度关注图像中相隔较远区域，即为局部性。接下来对这两点进行数学描述。

限制多层感知机

本文讨论的图像为二维图像$X$，其隐藏层为$H$，二者具有相同的形状。输入图像和隐藏层中位置$(i,j)$处的像素分别记为$\left [ X \right ] _{i,j} ,\left [ H \right ] _{i,j} $。为使每个隐藏神经元都能接收到每个输入像素的信息，将参数从权重矩阵替换为四阶权重张量$W$。假设$U$包含偏置参数，则全连接层可表示为

\[\begin{aligned} [\mathbf{H}]_{i, j} &=[\mathbf{U}]_{i, j}+\sum_{k} \sum_{l}[\mathbf{W}]_{i, j, k, l}[\mathbf{X}]_{k, l} \\ &=[\mathbf{U}]_{i, j}+\sum_{a} \sum_{b}[\mathbf{V}]_{i, j, a, b}[\mathbf{X}]_{i+a, j+b} \end{aligned}\]

上式中，$W$到$V$的转换只是形式上的转换。因为两个四阶张量的元素之间存在一一对应的关系，只需要重新索引下标$(k,l)$，使得$k = i + a$、$l = j +b$。索引$a、b$通过正负偏移实现了移动覆盖整个图像。上市表明，对于给定位置$(i,j)$处的像素值，可以通过$x$中以该位置为中心对像素进行加权求和得到，权重为$V$。

平移不变性

平移不变性从数学角度看就是输入X的平移，应该仅仅导致隐藏层的平移，不会引起最终输出的平移，即输出$V$和$U$不依赖于$(i,j)$的值，且$U$一般是一个常数，则上式可简化为

\[\begin{aligned} [\mathbf{H}]_{i, j} =u+\sum_{a} \sum_{b}[\mathbf{V}]_{a, b}[\mathbf{X}]_{i+a, j+b} \end{aligned}\]

上式即为卷积（convolution），从式中可以看出，输出是由$(i,j)$附近的像素加权求和得到，且权重不依赖于$(a,b)$，即图像中的位置。

局部性

根据局部性原则，不应过度关注相隔较远的区域，因此应该对a和b的取值进行限制，即应有

\[\left | a \right | > \Delta , \left | b \right | > \Delta\]

为便于计算，令$[V]_{a,b} = 0$，则卷积可写为

\[[\mathbf{H}]_{i, j}=u+\sum_{a=-\Delta}^{\Delta} \sum_{b=-\Delta}^{\Delta}[\mathbf{V}]_{a, b}[\mathbf{X}]_{i+a, j+b}\]

上式表示一个卷积层（convolution layer），卷积神经网络是包含卷积层的一类特殊的神经网络。$\mathbf{V}$被称为卷积核（convolution kernel）或者滤波器（filter），表示权重参数。当图像处理的局部区域很小时，卷积神经网络与多层感知机的训练差异可能是巨大的：以前，多层感知机可能需要数十亿个参数来表示网络中的一层，而现在卷积神经网络通常只需要几百个参数，而且不需要改变输入或隐藏表示的维数。

参数大幅减少的代价是，每一层只能包含局部的信息，所有的权重学习都将依赖于归纳偏置。当这种偏置与现实相符时，我们就能得到样本有效的模型，并且这些模型能很好地泛化到未知数据中。但如果这偏置与现实不符时，比如当图像不满足平移不变时，我们的模型可能难以拟合我们的训练数据。

卷积

通过上式得出的卷积与数学中的卷积定义有一定出入。数学中对两个函数$(f,g:\mathbb{R}^d,\mathbb{R})$的卷积的定义为

\[(f * g)(\mathbf{x})=\int f(\mathbf{z}) g(\mathbf{x}-\mathbf{z}) d \mathbf{z}\]

直观上讲，数学上的卷积表示的是其中一个函数翻转后与另一个函数加坐标轴围成图形的面积，对于离散变量，卷积表示求和。当变量为离散时，上式可写为：

\[(f * g)(\mathbf{x})=\sum_{a} f(\mathbf{z}) g(\mathbf{x}-\mathbf{z})\]

对于二元函数，上式对应写为

\[(f * g)(\mathbf{i,j})=\sum_{a}\sum_{b} f(\mathbf{a,b}) g(\mathbf{i}-\mathbf{a},\mathbf{j}-\mathbf{b})\]

上式与上一节推导得出的卷积公式存在一定差别。差别在于最后为$i-a,j-b$还是$i+a,j+b$。因为$a,b$表示的是中心位置$i,j$附近的位置，因此可正可负，所以式中的正负没有区别，两式等价。

通道

前两节推导出卷积的定义，并对比了与数学上卷积概念的区别，然而上面推导考虑的是二维图像，输入为二维张量，对应于实际图像，为灰度图，张量中每个值对应的是该像素点处的像素值（比如0-255）。实际中，大部分图像为彩色图，彩色一般包含三种颜色，因此，其不能用二维张量表示，而应该是由高度、宽度和颜色组成的三维张量，前两维表示的是像素的空间位置，第三维表示是像素的多维表示（如颜色）。

此时输入应为$\left [ X \right ] _{i,j,k} $，卷积核也对应调整为$\left [ V \right ] _{a,b,c} $，隐藏层也对应采取三维张量。对每一个空间位置，都应该采用一组而不是一个隐藏表示，每个隐藏表示称为通道（channel）或特征映射（feature maps），为后续层提供一组空间化的学习特征。

以$1024 \times 1024 \times 3$像素的三原色彩色图像和$1024*1024$像素的灰度图为例，对于灰度图，隐藏层的输入$H_2$可以由上面推导的二维卷积$C_2$确定，即$H_2 = C_2$。而对于彩色图像，其隐藏层的输入$H_3$应该由三维卷积$C_3$确定，而根据矩阵乘法可推知，三维卷积可以由一系列二维卷积的和求得，即应有如下关系：

\[C_3 = C_{21} + C_{22} + ... + C_{2n}\]

在本例中$n = 3$，$C_{21}、C_{22}、C_{23}$为三个通道，彩色图像的每个空间位置，都采用一组而不是一个隐藏表示，其中每个隐藏表示代表对应一种颜色的特征，即为后续层提供该颜色的学习特征。

根据上面的分析易知，此时的输出应表示为

\[[\mathrm{H}]_{i, j, d}=\sum_{a=-\Delta}^{\Delta} \sum_{b=-\Delta}^{\Delta} \sum_{c}[\mathrm{~V}]_{a, b, c, d}[\mathrm{X}]_{i+a, j+b, c}\]

其中，$d$表示输出通道，此式得到的输出将作为三维张量输入进入下一个卷积层。

图像卷积

互相关运算

严格来说，卷积层是个错误的叫法，该运算应该叫做互相关运算（cross-correlation），即输入张量与卷积核张量通过互相关运算产生输出张量。为简单起见，以二维张量为例，说明互相关运算的情况，输入为$2 \times 2$的二维张量，卷积核为$2 \times 2$的二维张量（其形状由内核的高度和宽度决定），具体如下图。

上图中阴影部分为第一个计算的输出元素，以及对应的输入元素和核元素。根据矩阵乘法，易知输出元素为：

\[0 \times 0+ 1 \times 1+ 3 \times 2+ 4 \times 3 = 19\]

运算过程中，卷积窗口从输入张量的左上角开始，从左到右，从上到下滑动。当卷积窗口滑动到新一个位置时，包含在该窗口中的部分张量与卷积核张量进行按元素相乘，得到的张量再求和得到一个单一的标量值。

从图中可以看出输出大小略小于输入大小。因为卷积核宽和高都大于1，而卷积核与矩阵边缘元素无法进行计算，所以输出大小应为输入大小减去卷积核大小后再加1。

卷积层

卷积层对输入和卷积核进行互相关运算，并在添加偏置（如果有）之后产生输出。所以卷积层的参数为卷积核权重和标量偏置。类似于多层感知机，训练卷积层时，也应该随机初始化卷积核。

特征映射和感受野

上文中提到，输出的卷积层又是也被称为特种证映射（feature map），因此也被视为输入映射到下一层的空间维度转换器。在CNN中，对某一层的任意元素$x$，感受野（receptive field）是指在前向传播期间可能影响$x$家孙的所有元素（来自于所有先前层）。感受野的覆盖率可能大于某层输入的实际大小，因此，当一个特征图中的任意元素需要检测更广区域的输入特征时，可以构建一个更深的区域。

填充和步幅

填充

应用多层卷积时，常常丢失边缘像素，因为使用的卷积核较小，所以尝尝只丢失几个像素。但是如果连续使用卷积层，累计丢失的像素会变多。所以解决的简单办法是填充（padding）：在输入图像的边缘填充元素（通常是填充0，不会影响卷积结果）。

当卷积核的高度或宽度为奇数时，可以在两侧分别填充一半的待填充行数，如果高度或宽度为偶数时，可以在一层填充所有的待填充行数。因此，一半卷积核的高度或宽度为奇数，既可以保持空间维度，也可以在顶部或底部填充相同数量的行，在左侧或右侧填充相同数量的列。

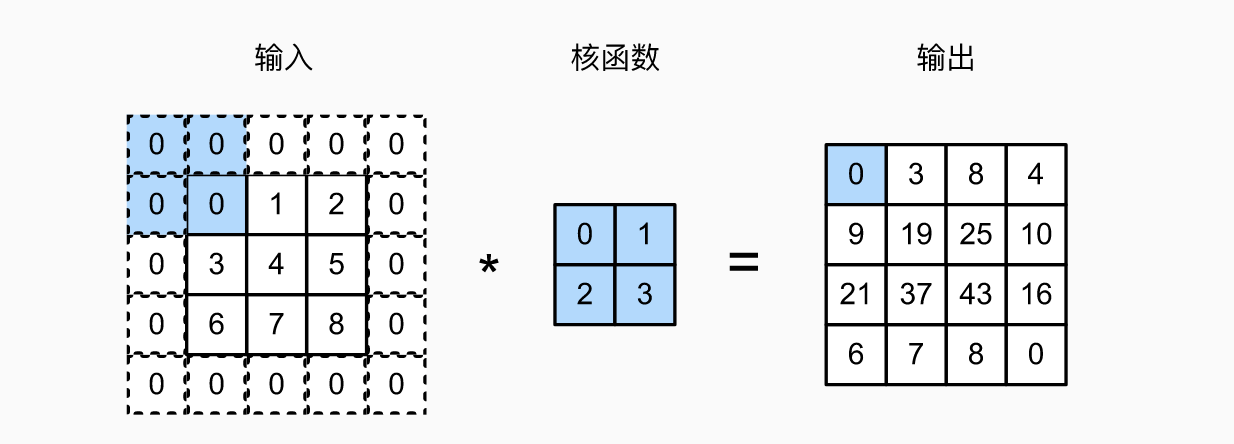
步幅

在计算互相关时，卷积核从左上角向右向下移动。前面的例子中，默认每次滑动一个元素，但有时为了高效计算或者缩减采样次数，卷积可以跳过中间位置，每次滑动多个元素，每次滑动元素的个数称为步幅（stride），通过填充和步幅可以有效调整数据的维度

明天就是平安夜，祝平安夜快乐！:-)