本文介绍卷积神经网络的第二部分。

多输入多输出通道

多输入通道

当输入包含多个通道时，需要构造一个与输入数据具有相同通道数的卷积核，以便进行互相关运算。假设输入的通道数为$c_i$，则卷积核的输入通道数也应为$c_i$。

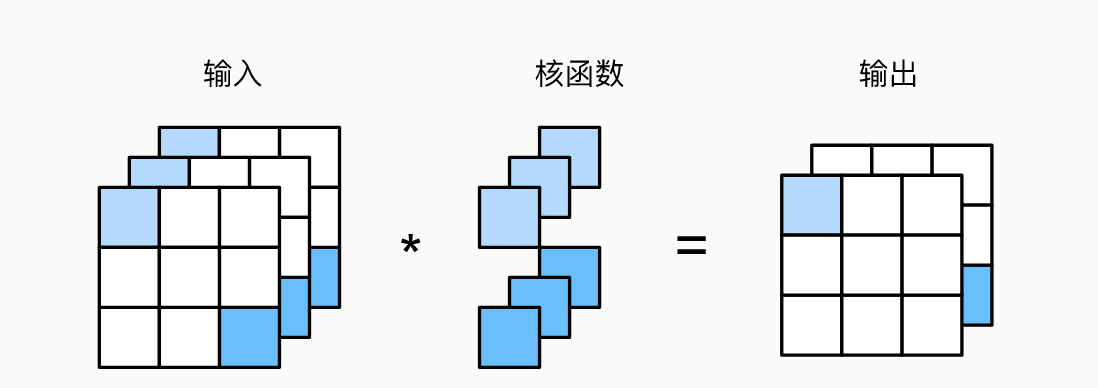
如果卷积核的窗口形状时$k_h \times k_w$，则卷积核可以看做$k_h \times k_w$的二维张量。如果$c_i$大于1时，卷积核的通道数也应为$c_i$，将每一个通道的张量连结在一起构成卷积核。此时如果进行二维互相关运算，可以对每个通道输入的二维张量和卷积核的二维张量进行互相关运算，再对每个通道的结果求和，具体如下图。

多输出通道

上文中提到输入通道可能有多个，但输出通道只有一个，然而实际中输出通道可能不止一个。随着神经网络层数的加深，常会增加输出通道的维数来减少空间分辨率以获得更大的通道深度。直观地说，可以将每个通道看做不同特征的响应，然而实际上通道之间不是独立的，所以多输出通道并不仅是多个单通道的简单组合。

用$c_i$和$c_o$分别表示输入和输出通道的数目，并用$k_h$、$k_w$表示卷积核的高度和宽度。此时对应多输出通道，所以为每个通道创建$c_i \times k_h \times k_w$的卷积核张量，则总的卷积核的形状为$c_o \times c_i \times k_h \times k_w$。在互相关运算中，每个输出通道先获取所有输入通道，再已对应的卷积核计算结果。

1*1卷积层

$1 \times 1$卷积层使用了最小窗口，使其失去了卷积层的特有能力——在高度和宽度维度上，识别相邻元素间相互作用的能力。下图展示了使用$1 \times 1$卷积核与3个输入通道与2个输出通道的互相关计算。

此时输入和输出具有相同的高度和宽度，输出的每个元素是输入中同一位置元素的线性组合，所以可以将该卷积层看做每个像素位置应用的全连接层。此卷积层常用来调整网络层的通道数量和控制模型复杂度。

汇聚层

进行图像处理时，我们希望逐渐降低隐藏层的空间分辨率聚集信息，这样随着神经网络中层叠的上升，每个神经元对其敏感的感受野（输入）就越大。而整个任务通常跟全局图像有关，所以最后一层应该对整个输入全局敏感，通过逐渐聚合信息，生成越来越粗糙的映射，最终实现学习全局表示的目标，同时将卷积图层的所有优势保留在中间层。此外，当检测较底层的特征时，我们通常希望这些特征保持某种程度上的平移不变性。例如，如果我们拍摄黑白之间轮廓清晰的图像$X$，并将整个图像向右移动一个像素，则新图像$Z$的输出可能大不相同。而在现实中，随着拍摄角度的移动，任何物体几乎不可能发生在同一像素上。为了解决上述问题，引入汇聚层（pooling），既可以降低卷积层对位置的敏感性，又可以降低对空间降采样表示的敏感性。

最大汇聚层和平均汇聚层

汇聚层由一个固定形状的窗口组成，窗口根据步幅大小在输入的所有区域滑动，并在每个位置计算一个输出。然而，不同于卷积层中输入和卷积核之间的互相关操作，汇聚层不包含参数。我们通常计算汇聚窗口中所有元素的最大值或平均值，这种操作分别称为最大汇聚层（maximum pooling）和平均汇聚层（average pooling）。

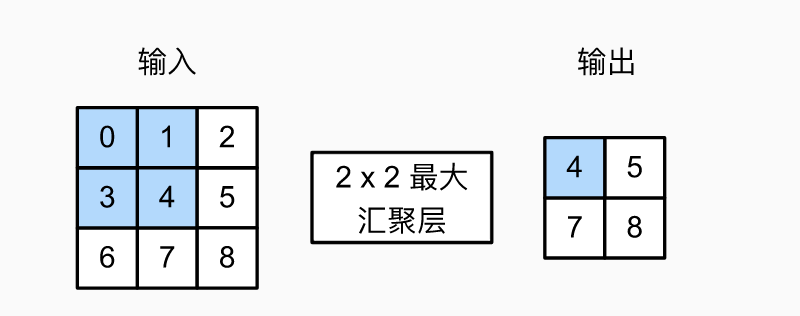
如下图所示，汇聚层运算符与卷积相似，都是从左上向右向下移动，在窗口内进行取最大值或平均值操作，哪种操作取决于使用平均值汇聚层还是最大值汇聚层。

填充和步幅

与卷积层类似，汇聚层也可以通过填充和步幅改变输出形状。默认情况下，步幅与窗口的大小相同，即如果使用形状为$(3,3)$的汇聚窗口，则得到的步幅形状为$(3,3)$。

填充和步幅可以手动设定。pool2d = nn.MaxPool2d(3, padding = 1, stride = 2)

也可以手动设定汇聚窗口，并设定填充和步幅的高度和宽度。

pool2d = nn.MaxPool2d((2,3), stride = (2,3), padding = (0,1))

多个通道

多通道输入时，汇聚层在每个通道单独计算，而不是像卷积层一样在通道上对输入进行汇总，即汇聚层的输出通道数与输入通道数相等。

卷积神经网络（LeNet）

LeNet可分为两部分：卷积编码器和全连接层密集块。卷积编码器由两个卷积层组成，全连接层密集块由三个全连接层组成。

每个卷积块中的基本单元是一个卷积层、一个sigmoid激活函数和平均汇聚层。请注意，虽然ReLU和最大汇聚层更有效，但它们在20世纪90年代还没有出现。每个卷积层使用$5 \times 5$卷积核和一个sigmoid激活函数。这些层将输入映射到多个二维特征输出，通常同时增加通道的数量。第一卷积层有6个输出通道，而第二个卷积层有16个输出通道。每个$2 \times 2$池操作（步骤2）通过空间下采样将维数减少4倍。卷积的输出形状由批量大小、通道数、高度、宽度决定。

为了将卷积块的输出传递给稠密块，我们必须在小批量中展平每个样本。换言之，我们将这个四维输入转换成全连接层所期望的二维输入。这里的二维表示的第一个维度索引小批量中的样本，第二个维度给出每个样本的平面向量表示。LeNet的稠密块有三个全连接层，分别有120、84和10个输出。因为我们仍在执行分类，所以输出层的10维对应于最后输出结果的数量。

在卷积神经网络中通常组合使用卷积层、非线性激活函数和汇聚层，为了构造高性能的网络，通常对卷积层进行排列，逐渐降低其表示的空间分辨率，同时增加通道数。